Basics¶
In this section, we cover the basic concepts employed within Wallace, focusing on those relating to evolutionary algorithms, and less on any other concepts concerned with other meta-heuristics supported within the framework.
For now, this section assumes that the reader has at least a basic knowledge of the structure and concepts of evolutionary algorithms.
Algorithm¶
The domain-specific language within Wallace is entirely tailored around the
specification and subsequent fine-tuning of algorithms for particular problem
instances. Users provide a specification of their problem to a particular
algorithm constructor, chosen according to the search algorithm they wish to
use to solve the problem, which is then composed into a heavily optimised
Algorithm instance via the compose! method, before being ready for
executed using the run! method.
Wallace supports a number of different meta-heuristic algorithms, ranging from random walks and hill climbing, to ant colony optimisation and evolutionary algorithms. For the remainder of this section however, we shall focus our discussion on the implementation of evolutionary algorithms within Wallace. More details about the other types of algorithms supported within Wallace may be found in the reference section of the documentation.
Evolutionary Algorithms¶
Brief recap.
Population¶
Abstractly, the population of the algorithm is used to hold the individuals which are presently alive within the current generation, as well as the offspring born within that generation. Each individual within the population is used to represent a candidate solution to the problem being solved.
Like many other evolutionary computation frameworks, Wallace models the population of an algorithm as a set of demes, or sub-populations, each containing a (nearly) isolated collection of individuals. Within each deme, all individuals belong to the same species, but within the population, each deme may elect to use a different species.
Simple Populations¶
For simple problems, one can use the population.simple model to quickly specify
a single deme population, which effectively hides the inner details of the deme
model from the user.
Complex Populations¶
The full power of the deme model can be utilised with the
population.complex model, which allows the user to add an arbitary number
of heterogeneous demes to the population. This ability can be exploited to
spread the search across multiple physical machines, or to allow the search to
test different problem representation and search parameters at the same time.
Island Model¶
Where the complex population model is employed, one may also choose to make use of an island model population.
In island model populations, each deme is conceptualised as a island within some imaginary archipelago, where all the individuals in that deme are confined to that island.
- After a certain number of generations, known as the migration interval, a pre-determined number, or fraction of individuals from each island may migrate from their island to a neighbouring island.
- The islands that an individual may migrate to from their current island is determined by the migration topology, which describes the connections between islands. By default, a fully connected topology is used, where every island can be reached by any other.
- The individuals selected to leave an island, and those chosen to be removed from an island to make room for them, are both decided according to a pre-determined migration policy.
An example of a simple island model population for the one max problem is shown below:
EXAMPLE CODE
Species¶
The species of an individual describes the fitness scheme it uses to transform the raw objective function values produced by the evaluator into fitness values, as well as each the high-level details of its chromosomes, such as their type and any restrictions upon them.
Complex Species¶
Unlike most other evolutionary computation frameworks, Wallace implements a multiple representation individual model, where each individual may be represented in a number of different ways (in fact, to our knowledge, no other framework implements a similar model). This feature allows stages of development to be codified, where one chromosome is used to produce another, which is then used to produce another, and so on, until a phenome is produced.
This ability comes in use when performing grammatical evolution, where an individual is subject to a process of development:
- Each individual begins life as a variable length bit string.
- From this bit-string, a series of codons, or non-terminal choices, are produced, by transforming each successive block of n bits into an integer.
- This series of codons is then used in conjuction with a provided grammar to produce a derivation, modelled as a string.
- Finally, if we are using grammatical evolution to evolve programs, this string is compiled to a program in the target language.
In Wallace, each of these stages can be explicitly modelled as its own developmental stage, as shown in the example below:
species.complex() do sp
sp.fitness = fitness.scalar()
sp.stages = [
species.stage("bit_string", representation.bit_string()),
species.stage("codons", "bit_string", True, representation.int_list()),
(species.stage("derivation", "codons") do stage
stage.representation = representation.grammar_derivation() do g
g.grammar = ...
end
end),
species.stage("executable", "derivation", executable.cpp())
]
end
Conversion¶
Conversion between stages is automatically handled by Wallace, according to transformation functions provided by the source and destination representations.
Most conversions operate by handling each chromosome in sequence, however some representations may make use of Wallace’s ability to perform mass conversion, where all chromosomes are handled within a single method call. This functionality can be useful when each conversion involves a certain degree of overhead that can otherwise be minimised by bundling it with others. This ability is used to compile Java and C programs concurrently, significantly reducing the not inconsiderable cost of conversion.
Mutation and Crossover¶
This multiple representation model of individuals also allows mutation and crossover to target different stages of development, rather than being restricted to act only the genotype. More details on the breeding of complex individuals is given in the Breeding section below.
Simple Species¶
As well as its complex species model, Wallace also offers a simpler species
model, species.simple, which hides the details of the multiple
representation model from the user, using its provided representation as the
sole developmental stage of the individual. For most problems, this model will
suffice.
An example of a simple species is given below:
species.simple() do sp
sp.fitness = fitness.scalar()
sp.representation = representation.int_vector(100)
end
Individual¶
Having discussed Wallace’s multiple representation model in the previous section, we now turn our attention to the slightly different individual model used in Wallace. Almost all other EC frameworks implement some parametric or base Individual class to model its individuals, representing fitness and genome as properties of the class, as shown below.
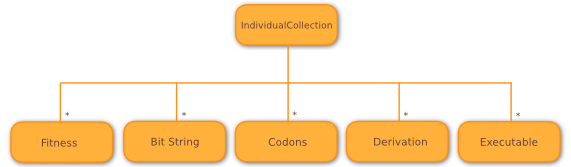
Instead, Wallace models individuals implicitly, using IndividualCollection objects,
containing separate arrays to hold fitnesses and different developmental stages of
all individuals within that collection, as shown below. All arrays are kept in sync, such that
the n-th entry in the fitness array belongs to the n-th entry in each of
the developmental stage arrays.
By implementing the individual model in such a way, we see a slightly enhanced performance, most likely due to a reduced number of cache misses, as developmental stages tend to be accessed at the same time as one another (during mutation and crossover). More importantly, this change allows us to implement the multiple representation model in a simple, easy-to-use manner, without affecting extensibility or performance.
Fitness¶
The calculation of fitness values within Wallace also differs slightly from a
number of other popular EC frameworks. Rather than having the evaluator return
a fitness value (whether it be a fitness object or a floating point value), the
evaluator makes use of a provided FitnessScheme to compute the fitness values
for individuals from an arbitary number of objective function values via the
assign function, as shown below:
assign(scheme, score)
This assign function returns a fitness value, based on the provided objective
function values, whose type is dependent on the fitness scheme being used (where
smaller, more efficient types are preferred over redundant objects). Once all
individuals have had an initial (possibly partial) fitness value assigned, the
complete set of fitness values (for both the offspring and existing members) is
passed to the scale! method, which transforms any partial fitness values into
full fitness values, relative to the contents of the deme.
Through its fitness schemes, Wallace provides support for a wide variety of multiple objective techniques, as well as co-evolution, fitness sharing, niching, crowding, and more. For more details on these techniques, please refer to the Reference section of the documentation.
Breeding¶
Breeding within Wallace is performed through a sub-type of the aptly named
breeder component. The exact processes involved depend on which type of
breeder is employed, however, all involve a process of selection, aided by
one or more selection operators, followed by a number of crossover
and mutation operators. Variation operators, i.e. crossover and
mutation, may operate on different developmental stages to one another;
Wallace takes care of ensuring everything is synchronised in the most
efficient way possible (with the help of meta-programming and analysis).
For a detailed list of the different breeding systems within Wallace, please refer to the reference section of the documentation.
Replacement¶
Following the process of breeding, evaluation, and possibly migration, each
deme is subject to a process of replacement, or survivor selection, wherein the
members of the next generation are decided from the current members of the deme
and their offspring. By default the replacement scheme is set to use generational
replacement, replacement.generational, where the entirety of the existing
deme contents are replaced by the complete set of offspring, as in the simple
genetic algorithm.